Z-order curve,1966年就已经在应用了。但是在大数据崭露头角,似乎才是这几年的事情。最近看了数据湖的一些技术,想从细处着手,介绍下我理解的 Z-Order.
1. 背景
Z-Order 在地图的场景中应用非常常见,比如查找地图上某个点附近的信息。
假定我们的地图数据里有 N 个点,记录了对应的位置坐标(经纬度)、id、名称、信息等,要查找当前坐标附近 10 公里内的餐馆。最朴素的想法就是计算所有餐馆跟当前位置的距离,过滤 <= 10 公里的结果。不过数据量大肯定不行,太多的冗余计算了。
按照我的理解,坐标轴天然是递增的,所以二分法是一个不错的解决方案:如果在一维世界(x维度),创建一个 x->id 的辅助数组,性能足够。类比到二维世界(x、y维度),通过创建 x->id、 y->id 两个辅助数组,两次二分查找,然后取交集。
这个方案仔细想想还是会有很多冗余计算,比如我想查找北航附近1公里的餐馆,没必要横竖都跨整个地球然后取交集出来。
一种自然的想法就是:我们可以先过滤满足海淀区这个条件。
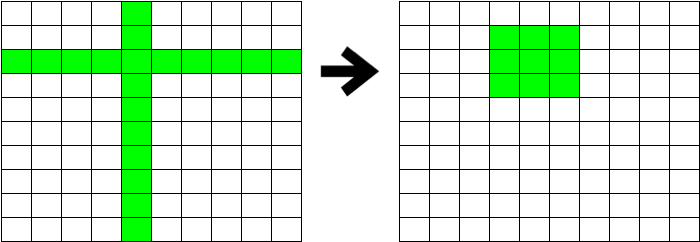
粗略的看,就是把两条纵横搜索,优化为单个区域的搜索,降低了搜索范围。
进一步,如果能够把二维坐标打平到一维,就可以复用一维的优化方案。打平可以用 GeoHash,也可以用 Morton Code,也就是 Z-Order.
例如各个景点对应的 Morton Code
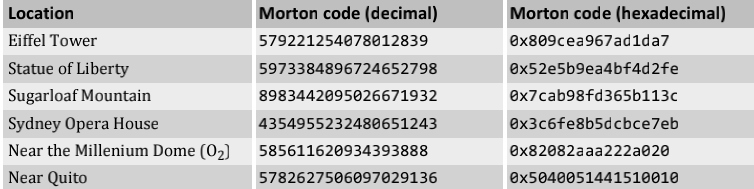
因此,我们可以说,Z-Order 就是一种多维打平到一维的算法。
2. Data Skipping
上述的想法,到了大数据领域,对应了 Data Skipping 这个听上去很高深的概念。
实际上上述地图查找,等价于如何优化如下 SQL 的执行过程:
WHERE x between (BASE_X - Delta, BASE_X + Delta) AND y between (BASE_Y - Delta, BASE_Y + Delta)
记得之前做阿拉丁的时候,用传统数据库,加速查询的方式是创建索引,几百万的数据量索引不是问题。
但是数据量大了之后,很难建立一个全局的索引。后来在 Spider,Bigtable 用的比较多,会非常注重 rowkey 的设计,确保充分利用全局有序的特性。本质上是为了追求高吞吐而采用 LSM-Tree,因此只能放弃 B+Tree.
此时要加速查询,一个有效的办法就是 DataSkipping:通过减少不必要的 IO 来提升查询速度。
比如 Hive 分区,就是把相同分区的数据放到相同目录下来减少参与 IO 的文件。
小文件合并减少需要读取的文件数、上一节提到的先过滤海淀区的餐馆,也都是一种 Data Skipping 的思路。
又比如统计文件字段的 min max,建立 BloomFilter 等。(跟 leveldb 这种小型的单机数据库的思路是一致的,只不过 leveldb 考虑的是尽可能读取 L0 的文件、通过 BloomFilter 过滤 datablock,而这里是过滤文件)
因此,给定过滤条件,如何尽可能少的筛选出来待读取的文件,是评价一个算法好坏的原则。
3. What is Z-Order
Z-Order 形状如图所示:
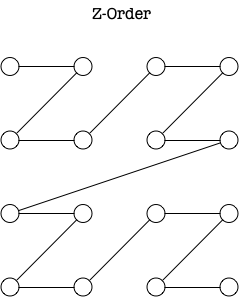
我最开始了解 Z-Order 时,好奇的是同样是二维打平到一维,为什么不是这样 Linear-Order:
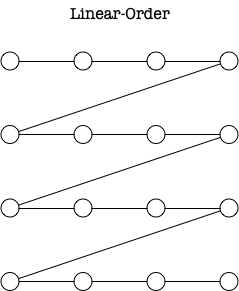
比如SQL Server - Custom Indexing for Latitude-Longitude Data,采用的就是将经纬度均分然后线性顺序自增值的方式。
相比介绍清楚 What is Z-Order,我觉得搞清楚为什么是 Z-Order 而不是其他比如 Linear-Order 同样重要。
其实本质还是上一节的目标:是否能够筛选出来更少的待读取的文件。通过 DataBricks 的这篇ZORDER Clustering 里的对比:
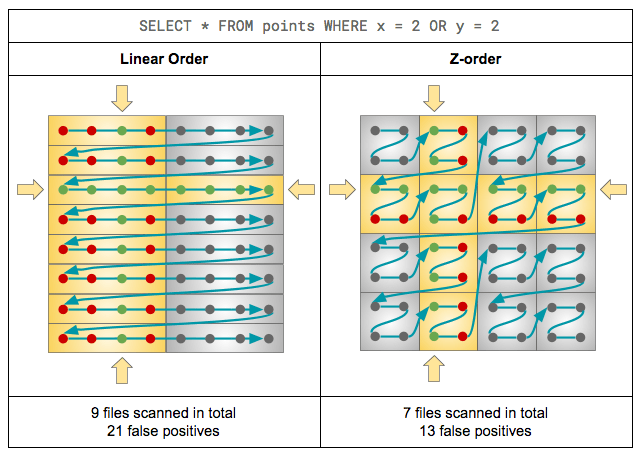
可以看到在这种条件下 ZOrder 方式参与 IO 的文件会更少一些。
Z-Order 的实现,文章已经很多了,不再赘述,可以参考:
4. Z-Order traverse
假定我们的查找条件为: x∈[2, 3] && y∈[4, 5],此时恰好组成一个 Z 型,只要顺序查找 36 -> 39 对应的所有文件即可。
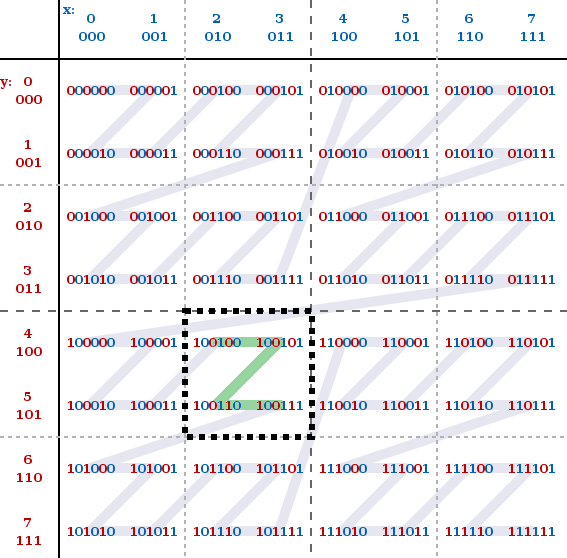
但实际情况往往会复杂很多,假定查找条件为:查找条件为: x∈[1, 3] && y∈[3, 4],需要顺序查找 11 -> 37 的全部文件
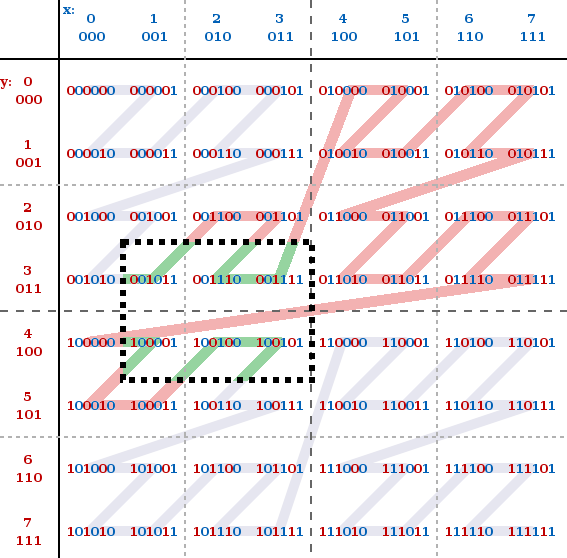
也就是红色的 Z 线是可能的查找范围,绿色 Z 线是目标查找范围,此时就需要优化遍历算法来尽可能的贴近绿色 Z 线,以降低参与 IO 的文件。
我在看 Z-Order curve 的 wiki 时,有一处和这里相同的疑问:https://stackoverflow.com/questions/30170783/how-to-use-morton-orderz-order-curve-in-range-search,也就是选定待遍历的 Z 曲线的 min/max 后,如何进一步优化遍历规则。由于本身更多只是使用 Z-Order,因此没有深入了解,感兴趣的可以参考附录里的内容。
5. Z-Order 应用
由于 Z-Order 满足分形的特性

最小的 Z ,是按照 NW,NE,SW,SE 的顺序遍历;扩大范围,Z跟Z之间也还是这个顺序。
因此在实际应用时,每个文件可以对应一个正方形的数据范围,根据实际需要的文件大小确定正方形包含了多少个 Z,然后记录每个文件对应的 Z 值 min max.
在阿里云的通过文件管理优化性能 通过一个例子描述了 Z-Order 的效果。
6. Z-Order Gotchas
印象里之前有个高T提过,其实现在硬件变化不大的现状下,无论是生产实践还是论文,都是在针对某些具体领域做优化,很难有“万金油”的绝对优化准则了。类似的优化,还有protobuf的varint编码也是基于实践中发现实际用到的整数都比较小,而 varint 基于小整数有非常好的存储优化效果。
我个人觉得这类是概率型的数据结构(类似跳表),实际情况比较大的概率能够调优,而不是类似索引一定能够加速查询,使用前应该有清楚的认知。