leveldb 的filter block用到了 filter policy,其中默认提供的是BloomFilterPolicy,即布隆过滤器,这篇笔记聊聊布隆过滤器的理论和在 leveldb 里的实现。
1. 简介
bloom filter是一种数据结构,作用类似于 hash table,相对于后者,空间利用率更高。
不过这种高利用率是有代价的,当我们在 bloom filter 查找 key 时,有返回两种情况:
- key 不存在,那么 key 一定不存在。
- key 存在,那么 key 可能存在。
也就是说 bloom filter 具有一定的误判率。
2. 理论知识
先介绍下 bloom filter 的几个组成:
- n 个 key
- m bits 的空间 v,全部初始化为0
- k 个无关的 hash 函数:
h1, h2, ..., hk,hash 结果为{1, 2, ..., m} or {0, 1, ..., m-1})
具体的,对于 key=a,经过 k 个 hash 函数后结果为
h1(a), h2(a), ..., hk(a)
那么就将 v 对应的 bit 置为 1.
假定 k 为 4,对应的 bloom filter 为:

注:这里有一个js写的一篇博客,支持互动的查看 bloom filter,更形象一些.
当 key 越来越多,v 里置为 1 的 bits 越来越多。对于某个不存在的 key’,k 个 hash 函数对应的 bit 可能正好为1,此时就概率发生误判,更专业的术语称为 false positive,或者 false drop.
因此,我们称 bloom filter 是一种概率型的数据结构,当返回某个 key’ 存在时,只是说明可能存在。
m 越大,k 越大, n 越小,那么 false positive越小。
更进一步,bloom filter 是关于空间和 false positive 的 tradeoff,bloom filter 的算法其实并不复杂,其真正的艺术在于这种平衡。
我们先看下 tradeoff 的结论:
hash 函数 k 的最优个数为 ln2 * (m/n).
3. 数学推导
这一节是数学推导上面的结论部分,主要是理论补充,也可以跳过直接看下一节的实现部分。
接着 bloom filter 的组成讲,对一个指定的 bit,其被设置为0、1的概率分别为
P(1) = 1/m
P(0) = 1 - 1/m
k 个 hash 函数,该 bit 设置为 0 的概率为
P'(0) = P(0) ** k = (1 - 1/m) ** k
再经过 n 个 key,该 bit 设置为 0 的概率为
P''(0) = P'(0) ** n = (1 - 1/m) ** kn
而根据自然对数 e 的计算公式
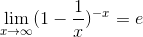
我们可以近似计算前面的P''(0)
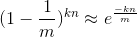
对应的,P''(1)的概率为:
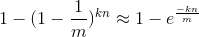
附注,关于自然对数 e 的值:
| x | (1 - 1/x) ** (-x) |
|---|---|
| 4 | 3.160494 |
| 16 | 2.808404 |
| 64 | 2.739827 |
| 256 | 2.723610 |
| 1024 | 2.719610 |
| 4096 | 2.718614 |
| 16384 | 2.718365 |
| 65536 | 2.718303 |
| 262144 | 2.718287 |
| 1048576 | 2.718283 |
| 4194304 | 2.718282 |
当检测某个实际不存在的 key 时,满足条件:
其对应的 k 个 bit 恰好都设置为了1,此时即 false positive 的场景。
概率为:
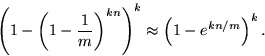
问题是,怎么最小化 false_positive 呢?
为了简化描述,先定义 p (即P''(0):某个 bit 设置为0的概率):
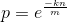
那么
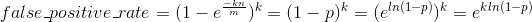
底数是 e,为固定值,那么最小化 false_positive_rate 即为最小化指数g = k * ln (1 − p)
结合 p 的定义,k 值推导为
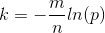
因此得到 g
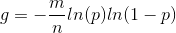
根据对称性,当 p = 1/2 时,f 取得最小值。此时k、f最小值为:
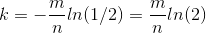
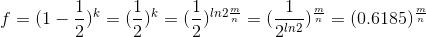
考虑到 p 为设置为0的概率,因此可以认为 m 有一半设置为1,一半设置为0时,误判率最低。
False positive rate 和 m/n、k 的组合关系表:
| m/n | k | k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | k=7 | k=8 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 1.39 | 0.393 | 0.400 | ||||||
| 3 | 2.08 | 0.283 | 0.237 | 0.253 | |||||
| 4 | 2.77 | 0.221 | 0.155 | 0.147 | 0.160 | ||||
| 5 | 3.46 | 0.181 | 0.109 | 0.092 | 0.092 | 0.101 | |||
| 6 | 4.16 | 0.154 | 0.0804 | 0.0609 | 0.0561 | 0.0578 | 0.0638 | ||
| 7 | 4.85 | 0.133 | 0.0618 | 0.0423 | 0.0359 | 0.0347 | 0.0364 | ||
| 8 | 5.55 | 0.118 | 0.0489 | 0.0306 | 0.024 | 0.0217 | 0.0216 | 0.0229 | |
| 9 | 6.24 | 0.105 | 0.0397 | 0.0228 | 0.0166 | 0.0141 | 0.0133 | 0.0135 | 0.0145 |
| 10 | 6.93 | 0.0952 | 0.0329 | 0.0174 | 0.0118 | 0.00943 | 0.00844 | 0.00819 | 0.00846 |
4. 代码实现
bloom filter 代码实现并不复杂,在 leveldb 有一个完整的实现,注释版的源码位于bloom.cc,对应类BloomFilterPolicy,主要有三个接口
- 构造函数
CreateFilter:根据传入的 keys,计算对应的 hash area.KeyMayMatch:查找传入的 key 是否存在
可以看到,bloom filter 仅支持插入和查找,不支持删除操作(导致误删除)。
构造函数主要是根据 m/n 计算 k 的个数,公式如上面推导,不过最大不超过 30 个:
//记录bits_per_key,计算最优的hash函数个数
explicit BloomFilterPolicy(int bits_per_key)
: bits_per_key_(bits_per_key) {
// We intentionally round down to reduce probing cost a little bit
// bits_per_key = m / n
// k_ = ln(2) * bits_per_key
k_ = static_cast<size_t>(bits_per_key * 0.69); // 0.69 =~ ln(2)
// [1, 30]个hash函数
if (k_ < 1) k_ = 1;
if (k_ > 30) k_ = 30;
}
hash 函数的选择上,leveldb 用了比较取巧的办法,只定义了一个 hash 函数:
static uint32_t BloomHash(const Slice& key) {
return Hash(key.data(), key.size(), 0xbc9f1d34);
}
注:虽然多次调用,函数间仍然保持independent,因此仍然满足前面的公式
CreateFilter计算传入的 n 个 key,最终结果存储到dst(对应到理论介绍里的 m)
首先计算需要的总字节数,然后依次调用 k 次 hash 函数,存储到dst,并在最后追加 k 本身。
virtual void CreateFilter(const Slice* keys, int n, std::string* dst) const {
// Compute bloom filter size (in both bits and bytes)
// 计算需要的bit数
size_t bits = n * bits_per_key_;
// For small n, we can see a very high false positive rate. Fix it
// by enforcing a minimum bloom filter length.
if (bits < 64) bits = 64;
//计算需要的bytes数,最少8bytes
size_t bytes = (bits + 7) / 8;
bits = bytes * 8;
//dst[init_size : init_size + bytes]写入过滤器内容,默认全为0
//dst[init_size + bytes]写入hash函数个数
const size_t init_size = dst->size();
dst->resize(init_size + bytes, 0);
dst->push_back(static_cast<char>(k_)); // Remember # of probes in filter
char* array = &(*dst)[init_size];//更新array <-> dst[init_size : init_size + bytes]
for (int i = 0; i < n; i++) {
// Use double-hashing to generate a sequence of hash values.
// See analysis in [Kirsch,Mitzenmacher 2006].
uint32_t h = BloomHash(keys[i]);
const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits
for (size_t j = 0; j < k_; j++) {
//计算并更新对应的bit为1
const uint32_t bitpos = h % bits;
array[bitpos/8] |= (1 << (bitpos % 8));
h += delta;
}
}
}
KeyMayMatch则是其逆过程,不再赘述
virtual bool KeyMayMatch(const Slice& key, const Slice& bloom_filter) const {
const size_t len = bloom_filter.size();
if (len < 2) return false;
const char* array = bloom_filter.data();
const size_t bits = (len - 1) * 8;
// Use the encoded k so that we can read filters generated by
// bloom filters created using different parameters.
const size_t k = array[len-1];
if (k > 30) {
// Reserved for potentially new encodings for short bloom filters.
// Consider it a match.
return true;
}
uint32_t h = BloomHash(key);
const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits
for (size_t j = 0; j < k; j++) {
const uint32_t bitpos = h % bits;
if ((array[bitpos/8] & (1 << (bitpos % 8))) == 0) return false;
h += delta;
}
return true;
}
5. 测试
补充下测试代码,能够更直观的看到BloomFilterPolicy这个类的接口用法
插入两个 key: “hello” “world”,然后通过KeyMayMatch查看是否存在
{
std::string dst;
const leveldb::Slice keys[2] = {"hello", "world"};
bloom_filter->CreateFilter(keys, 2, &dst);
std::cout << bloom_filter->KeyMayMatch(keys[0], dst) << std::endl;
std::cout << bloom_filter->KeyMayMatch(keys[1], dst) << std::endl;
std::cout << bloom_filter->KeyMayMatch("ufo exists?", dst) << std::endl;
std::cout << bloom_filter->KeyMayMatch("nullptr", dst) << std::endl;
}
看下误判率,leveldb 自带的单测代码有更完善的版本。
{
std::string dst;
std::vector<leveldb::Slice> keys;
for (int i = 0; i < 10000; ++i) {
keys.push_back(std::string(i, 'a'));
}
bloom_filter->CreateFilter(&keys[0], int(keys.size()), &dst);
int fail_count = 0;
for (int i = 0; i < 10000; ++i) {
if (bloom_filter->KeyMayMatch(std::string(i, 'b'), dst)) {
fail_count++;
}
}
std::cout << "try 10000 times, fail:" << fail_count << std::endl;
}