Ying

leveldb笔记之21:二分法

 
  • Mar 31, 2019

二分法是个很有意思的话题，思路很简单，也能极大的提高程序的性能，之前我们介绍过如何写出正确的二分法以及分析 。因为二分法在 leveldb 使用非常常见，这篇笔记炒个冷饭，再结合着 leveldb 源码讲下二分法最重要的一个概念：循环不变式。

1. Block 内的 Seek

当我们查找 target 是否存在于某个 data block，用的就是二分法，二分的对象是 restart points.

restart points 将 entry 分为多组：

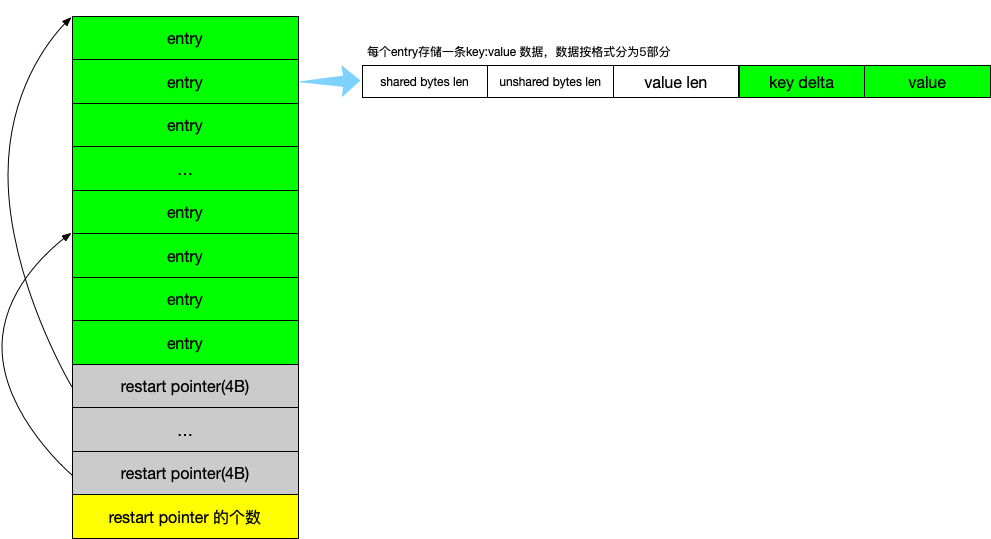
BlockBuilderLogic

每组包含多个key:value数据，每一个 restart point 指向一组里最小的那个 entry，我们称为 min-key entry.

Seek的目标是找到第一个 >= target 的 entry.

因此，我们需要先找到第一个 < target 的 min-key entry，然后不断Next直到 entry >= target.

可以推导出循环不变式：

  1. 如果mid_key < target，那么 target 一定位于[mid, right]区间里。
  2. 如果mid_key >= target，那么 target 一定位于[left, mid - 1]区间里。

代码也就容易理解了：

    // Binary search in restart array to find the last restart point
    // with a key < target
    uint32_t left = 0;
    uint32_t right = num_restarts_ - 1;
    //查找刚好 < target的restart point.
    while (left < right) {
      uint32_t mid = (left + right + 1) / 2;
      uint32_t region_offset = GetRestartPoint(mid);
      uint32_t shared, non_shared, value_length;
      //region_offset是一个restart point，因此:
      //shared = 0, non_shared就是key的长度, key_ptr指向的就是完整的key
      const char* key_ptr = DecodeEntry(data_ + region_offset,
                                        data_ + restarts_,
                                        &shared, &non_shared, &value_length);
      if (key_ptr == nullptr || (shared != 0)) {
        CorruptionError();
        return;
      }
      Slice mid_key(key_ptr, non_shared);
      if (Compare(mid_key, target) < 0) {
        // Key at "mid" is smaller than "target".  Therefore all
        // blocks before "mid" are uninteresting.
        left = mid;
      } else {
        // Key at "mid" is >= "target".  Therefore all blocks at or
        // after "mid" are uninteresting.
        right = mid - 1;
      }
    }

2. 查找文件

除了 level 0，其他 level 的文件都是有序的，每个文件有一个 key range: [smallest, largest].

struct FileMetaData {
  int refs;
  int allowed_seeks;          // Seeks allowed until compaction
  uint64_t number;
  uint64_t file_size;         // File size in bytes
  InternalKey smallest;       // Smallest internal key served by table
  InternalKey largest;        // Largest internal key served by table

  FileMetaData() : refs(0), allowed_seeks(1 << 30), file_size(0) { }
};

给定一层文件和待查找的 target，Seek的目标是查找 target 可能位于哪个文件。

结合文件的 key range，我们就是要查找第一个满足条件largest >= target的文件。可以推导出循环不变式：

  1. 如果mid_file.largest >= target，那么 target 一定位于[left, mid]区间里。
  2. 如果mid_file.largest < target，那么 target 一定位于[mid + 1, right]区间里。

具体的代码：

//二分查找第一个满足条件的file:file->largest>=key，如果key存在于files，那么一定存在于该file
//如果不存在则返回files.size()
//关于二分查找最重要的是loop invariant，可以参考之前写的笔记：https://izualzhy.cn/binary-search-analysis
//是不是可以用std::lower_bound ci && pull request?
int FindFile(const InternalKeyComparator& icmp,
             const std::vector<FileMetaData*>& files,
             const Slice& key) {
  uint32_t left = 0;
  uint32_t right = files.size();
  while (left < right) {
    uint32_t mid = (left + right) / 2;
    const FileMetaData* f = files[mid];
    if (icmp.InternalKeyComparator::Compare(f->largest.Encode(), key) < 0) {
      //f->largest比key要小，说明一定不在f以及之前的文件，接下来查找>f的文件
      // Key at "mid.largest" is < "target".  Therefore all
      // files at or before "mid" are uninteresting.
      left = mid + 1;
    } else {
      //f->largest >= key，说明一定在f或者之前的文件，接下来查找<=f的文件
      // Key at "mid.largest" is >= "target".  Therefore all files
      // after "mid" are uninteresting.
      right = mid;
    }
  }
  return right;
}
Search