
尽管是本入门书籍,不过仍然读的很慢,前后花了十几个小时。读这本书的时候,大学里高等代数里的矩阵乘法、秩的概念、最优化理论里的梯度下降、小波分析,楞是一点都想不起来🙈。
1. 感知机
感知机的想法很直白:
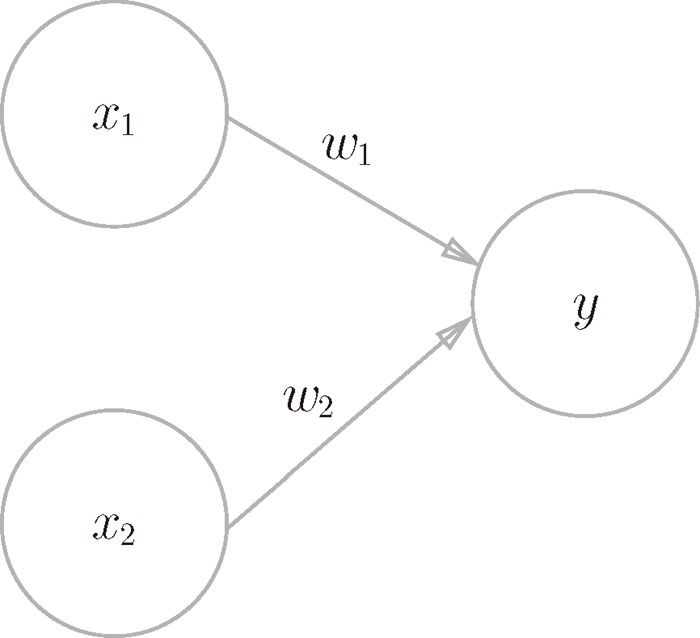
其中 x 是输入,w 是权重,θ是阈值。y 是输出,大于阈值输出 1,小于阈值输出 0.
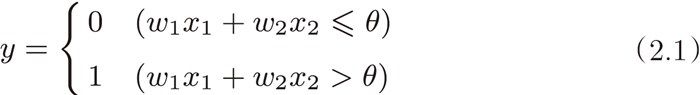
通过设置不同的权重和阈值,我们可以使用感知机实现与门(两个输入均为 1 时输出1,其他时候则输出 0)、与非门(跟与门相反)、或门(输入有 1 个是 1,输出就为 1)。
但是异或门无法用线性函数表示,需要用非线性函数或者多层感知机。
注:读到这里的时候,想到了《智慧的疆界》一书里:
明斯基在书中最后给出了他对多层感知机的评价和结论:“研究两层乃至更多层的感知机是没有价值的。”因此多层感知机在没来及被大家深入探究之前,就被明斯基直接判处了死刑。
2. 神经网络
实现与门需要手动配置权重,神经网络相比感知机,最核心的目标是自动生成权重值
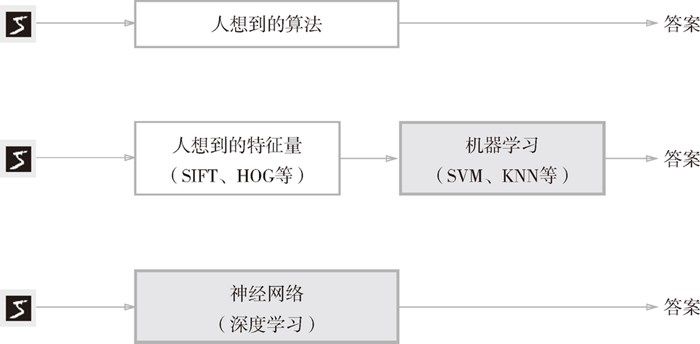
因此引入了几个概念:
激活函数:y=σ(W⋅x+b) ,表示神经元的输出,常见的例如 Sigmoid 函数。跟阶跃函数相比,相同点是其 y 轴取值范围、函数曲线的趋势都是一致的,不同点在于平滑程度,因此当微调权重的时候,函数值也会发生变化。
Sigmoid 函数的定义:\(\sigma(x) = \frac{1}{1 + \exp(-x)}\)
输出层所用的激活函数,要根据求解问题的性质决定。一般地,回归问题可以使用恒等函数,二元分类问题可以使用 sigmoid 函数,多元分类问题可以使用 softmax 函数。
训练数据(监督数据)和测试数据:使用训练数据进行学习,寻找最优的参数;使用测试数据评价训练得到的模型的实际能力,以追求模型的泛化能力。
损失函数:神经网络的学习中所用的指标称为损失函数(loss function),损失函数可以使用任意函数,但一般用均方误差和交叉熵误差。比如识别手写数字的场景,为什么不直接使用识别精度作为指标?本质上是避免导数为 0,使得微调产生效果,跟激活函数的思想类似。
梯度法:为了逐步降低损失函数的值,使用随机梯度下降法(SGD)来寻找最小值(或者尽可能小的值),这个过程就会不断地更新权重参数。梯度法有点像贪心算法,梯度是当前函数值减小最多的方向,因此迭代的过程是局部不断减少。但是,无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际上,在复杂的函数中,梯度指示的方向基本上都不是函数值最小处。
\[\mathbf{W} \leftarrow \mathbf{W} - \eta \frac{\partial L}{\partial \mathbf{W}}\]更新的权重参数记为\(\mathbf{W}\),损失函数关于 \(\mathbf{W}\) 的梯度记为 \(\frac{\partial L}{\partial \mathbf{W}}\), \(\eta\) 记为学习率,学习率(数学式中记为 η)的值很重要。学习率过小,会导致学习花费过多时间;反过来,学习率过大,则会导致学习发散而不能正确进行。实际取值为 0.01 0.001 等,这样就实现了不断更新权重查找“最小值”的效果。
3. 误差反向传播法
通过数值微分计算梯度的方法简单,但是耗时,而误差反向传播法则非常高效。
链式法则:如果某个函数由复合函数表示,则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。
反向传播:即由输出来反推输入,计算输入多大程度上会影响输出 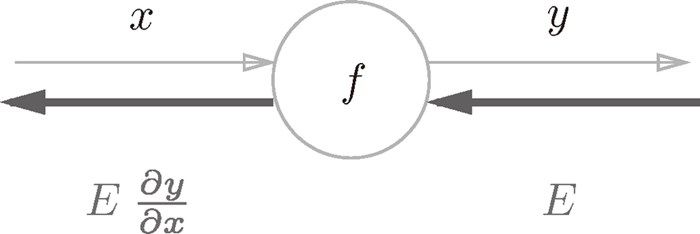
sigmoid 的反向传播公式: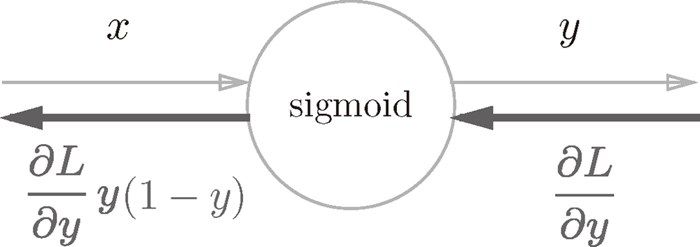
神经网络的学习步骤:
- mini-batch: 从训练数据中随机选择一部分数据
- 计算梯度: 计算损失函数关于各个权重参数的梯度
- 更新参数: 将权重参数沿梯度方向进行微小的更新
- 重复 1 2 3
相比来讲,误差反向传播法求梯度的效率更高。
注:这一节没太看懂,总体来说,感觉是一轮 forward 后,根据结果的偏差及每个节点的导数,来反推哪些节点的权重值要降低/升高,所以在实现里也需要记录 forward 输出的值。
4. SGD 的优化
SGD 方法对于呈延伸状的图形,比如:
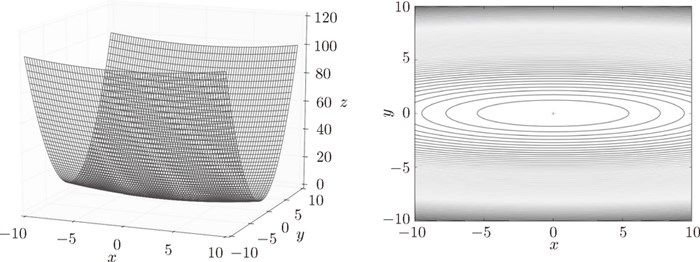
搜索时,呈“之”字形朝最小值 (0, 0) 移动: 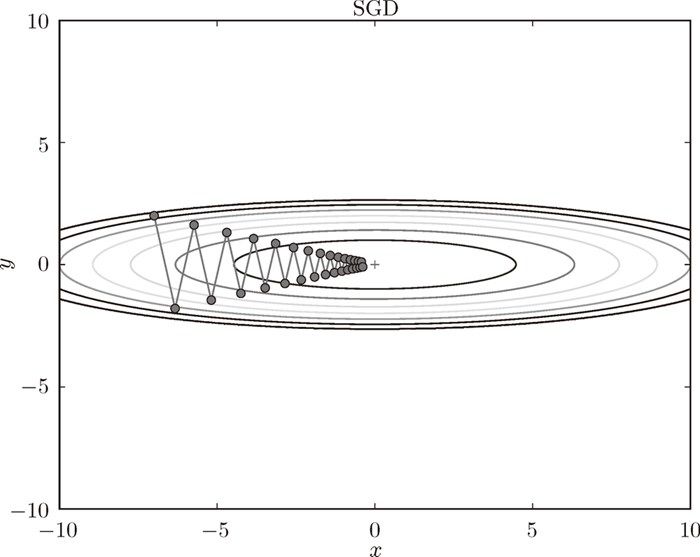
为了改正SGD的缺点,Momentum 公式引入了速度的概念,AdaGard 公式则引入学习率衰减,Adam 公式则融合了以上两者:
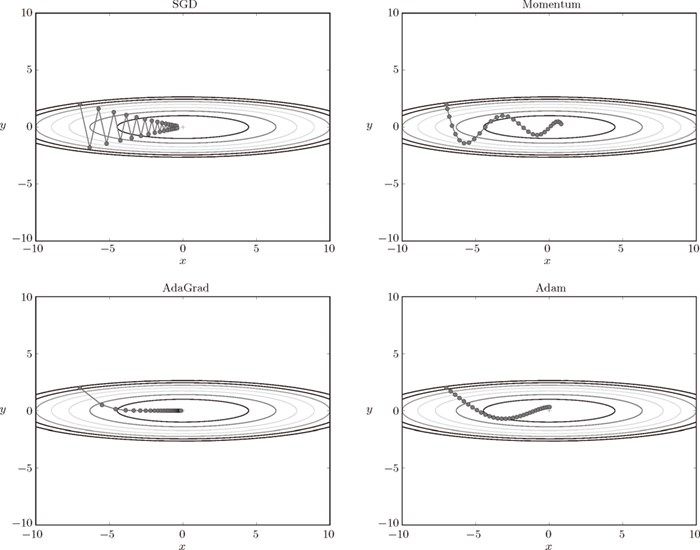
这 4 种方法各有各的特点,都有各自擅长解决的问题和不擅长解决的问题。
5. 总结
书里接下来介绍了卷积神经网络、强化学习等,包括权重初始值、损失函数最小值搜索算法、超参数,都需要根据实际情况摸索。以及一直在提斯坦福大学的课程 CS231n,不过我个人读这本书是希望能够听懂/看懂算法里常提到的名词,因此没有继续深入学习。有时候在想,如果在大学就学习这些课程,没准自己现在就是一名算法工程师了。
回到题目本身,作者提到了“What I cannot create, I do not understand.”,这种刨根问底的态度,我觉得是非常值得学习和保持的。