Ying

由两种遍历结果构造二叉树

 
  • Mar 26, 2014

还是二叉树遍历的题目，不过是由遍历结果反推二叉树。

两个题目是类似的，关于树的问题第一反映就是递归。以中序、后序推导为例，
中序结果为LNR,后序结果为LRN,因此可以通过后序结果的最后一个node(即根节点)，在中序结果中查找，就可以区分L,R，然后继续递归计算即可。

举个列子，假设二叉树为

       1
      / \
     2   3
    / \
   4   5

中序遍历为
4 2 5 1 3

后序遍历为
4 5 2 3 1

后序最后一个值为1,表示根节点，查找该节点在中序遍历的位置，左边为左子树，右边为右子树，即左子树中序遍历结果为
4 2 5
后序遍历结果为
3
根据左右子树的大小可以在后序遍历里找到对应的后序遍历结果。递归求解即可。

需要注意的是，过程中始终传递完整的二叉树的遍历结果并标明下在中序、后序的范围即可，如果每次都传对应子树的遍历结果递归，会很占内存。

图解

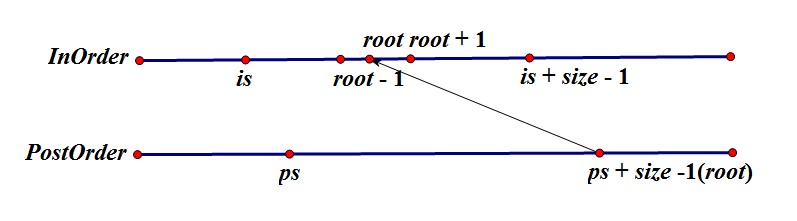
索引值的计算:
由图中可以理解，is,ps,size分别表示inorder,postorder的start位置，以及当前树的大小。
由PostOrder的ps + size - 1找到root,在InOrder里找到该root的位置，那么InOrder的左子树为[is, root-1],右子树为[root+1,is+size-1]。
根据左右子树的大小也可以求出PostOrder的位置，递归分别去构造左右子树就可以了。

PreOrder+InOrder 代码如下：

/*
 * =====================================================================================
 *       Filename:  construct-binary-tree-from-preorder-and-inorder-traversal.cpp
 *    Description:  http://oj.leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
 * =====================================================================================
 */

#include <iostream>
#include <vector>
using namespace std;

struct TreeNode
{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

TreeNode* buildTree(const vector<int>& preorder, int ps,
                    const vector<int>& inorder, int is,
                    const int treeSize)
{
    if (!treeSize)
    {
        return NULL;
    }

    int rootValue = preorder[ps];
    TreeNode* rootNode = new TreeNode(rootValue);

    int rootIndex = is;
    while (inorder[rootIndex] != rootValue)
        ++rootIndex;

    int leftTreeSize = rootIndex - is;
    int rightTreeSize = treeSize - leftTreeSize - 1;

    TreeNode* leftTree = buildTree(preorder, ps + 1, inorder, is, leftTreeSize);
    rootNode->left = leftTree;

    TreeNode* rightTree = buildTree(preorder, ps + leftTreeSize + 1, inorder, rootIndex + 1, rightTreeSize);
    rootNode->right = rightTree;

    return rootNode;
}

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
    return buildTree(preorder, 0, inorder, 0, preorder.size());
}

void print(TreeNode* node)
{
    if (node)
    {
        print(node->left);
        print(node->right);
        cout << node->val << endl;
    }
}

int main()
{
    int in[] = {4,2,5,1,3};
    int pre[] = {1,2,4,5,3};
    vector<int> a = vector<int>(in, in + 5);
    vector<int> b = vector<int>(pre, pre + 5);

    TreeNode* node = buildTree(b, a);
    print(node);

    return 0;
}

InOrder + PostOrder代码如下：

/*
 * =====================================================================================
 *    Description:  http://oj.leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/ 
 * =====================================================================================
 */
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

struct TreeNode
{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

TreeNode* buildTree(const vector<int>& inorder, const int is,
                    const vector<int>& postorder, const int ps,
                    const int treeSize)
{
    if (!treeSize)
    {
        return NULL;
    }

    int rootValue = postorder[ps + treeSize - 1];
    TreeNode* rootNode = new TreeNode(rootValue);

    int rootIndex = is;
    while (inorder[rootIndex] != rootValue)
        rootIndex++;

    int leftTreeSize = rootIndex - is;
    int rightTreeSize = treeSize - leftTreeSize - 1;

    TreeNode* leftNode = buildTree(inorder, is, postorder, ps, leftTreeSize);
    rootNode->left = leftNode;

    TreeNode* rightNode = buildTree(inorder, rootIndex + 1, postorder, ps + leftTreeSize, rightTreeSize);
    rootNode->right = rightNode;
    return rootNode;
}

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
    return buildTree(inorder, 0, postorder, 0, inorder.size());
}

void print(TreeNode* node)
{
    if (node)
    {
        cout << node->val << endl;
        print(node->left);
        print(node->right);
    }
}

int main()
{
    int in[] = {4,2,5,1,3};
    int post[] = {4,5,2,3,1};
    vector<int> a = vector<int>(in, in + 5);
    vector<int> b = vector<int>(post, post + 5);

    TreeNode* node = buildTree(a, b);
    print(node);

    return 0;
}

同样可以理解为什么由PreOrder/PostOrder无法构造二叉树，因为两种遍历结果都可以找到root值，这个功能重复，然而却都无法区分左右子树。

Search